Глава 2. Однородная система двух уравнений первой степени с тремя неизвестными

Пусть дана система двух однородных уравнений

, (1)

с тремя неизвестными x, y, z. Введем обозначения

, , .

Если хотя бы один из определителей , , не равен нулю, то все решения системы (1) будут определяться по формулам

, , ,

где t - произвольное число. Каждое отдельное решение получается при каком-либо определенном значении t.

Для практики вычислений полезно заметить, что определители , , 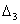получаются при помощи поочередного вычеркивания столбцов таблицы:

.

Если все три определителя , , равны нулю, то коэффициенты уравнений системы (1) пропорциональны. В этом случае одно из уравнений системы есть следствие другого и система фактически сводится к одному уравнению. Такая система, естественно, имеет бесконечно много решений; чтобы получить какое-нибудь из них, следует двум неизвестным придать произвольно численные значения, а третье найти из уравнения.

Текст издания:	© Д.В.Клетеник "Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998.
Решение задач:	© Кирилл Кравченко, http://a-geometry.narod.ru/. Все права принадлежат мне, если не оговорено иное ;-)