






Глава 23. Центр линии второго порядка
Линия, которая в некоторой
декартовой системе координат определяется
уравнением второй степени, называется линией
второго порядка. Общее уравнение второй степени
(с двумя переменными) принято записывать в виде:
 (1)
(1)
Центром некоторой линии называется
такая точка плоскости, по отношению к которой
точки этой линии расположены симметрично парами.
Линии второго порядка, обладающие единственным
центром, называются центральными.
Точка S( ,
,  ) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:
) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:
 ,
,  (2)
(2)
Обозначим через  определитель
этой системы:
определитель
этой системы:
 .
.
Величина  составляется из
коэффициентов при старших членах уравнения (1) и
называется дискриминантом старших членов этого
уравнения.
составляется из
коэффициентов при старших членах уравнения (1) и
называется дискриминантом старших членов этого
уравнения.
Если  , то система (2) является
совместной и определенной, то есть имеет решение
и притом единственное. В этом случае координаты
центра могут быть определены по формулам
, то система (2) является
совместной и определенной, то есть имеет решение
и притом единственное. В этом случае координаты
центра могут быть определены по формулам
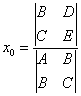 ,
, 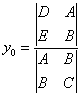 .
.
Неравенство  служит признаком
центральной линии второго порядка.
служит признаком
центральной линии второго порядка.
Если S( ,
,  ) - центр линии второго порядка,
то в результате преобразования координат по
формулам
) - центр линии второго порядка,
то в результате преобразования координат по
формулам
 ,
, 
(что соответствует переносу начала
координат в центр линии) ее уравнение примет вид

где A, B, C те же, что в
данном уравнении (1), а  определяется
формулой
определяется
формулой
 .
.
В случае  имеет место
также следующая формула:
имеет место
также следующая формула:
 ,
,
где
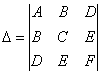 .
.
Определитель  называется
дискриминантом левой части общего уравнения
второй степени.
называется
дискриминантом левой части общего уравнения
второй степени.





| Текст издания: |
© Д.В.Клетеник "Сборник задач по
аналитической геометрии". М., Наука, Физматлит,
1998. |
 |
| Решение задач: |
© Кирилл Кравченко,
http://a-geometry.narod.ru/.
Все права принадлежат мне, если не оговорено иное ;-) |

Сайт управляется системой
uCoz![]()

![]()
![]()
![]() (1)
(1)![]() ,
, ![]() ) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:
) является центром линии,
определяемой уравнением (1), в том и только в том
случае, когда ее кординаты удовлетворяют
уравнениям:![]() ,
, ![]() (2)
(2)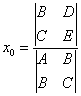 ,
, 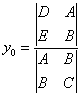 .
.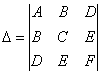 .
.