Глава 2. Декартовы прямоугольные координаты на плоскости

Декартова прямоугольная система координат определяется заданием линейной единицы для измерения длин и двух взаимно перпендикулярных осей, занумерованных в каком-нибудь порядке.

Точка пересечения осей называется началом координат, а сами оси - координатными осями. Первая из координатных осей называется осью абсцисс, вторая - осью ординат.

Начало координат обозначается буквой О, ось абсцисс - символом Ох, ось ординат - символом Оу.

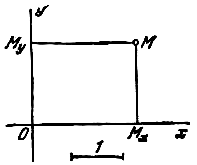
Координатами произвольной точки М в заданной системе называют числа

,

( см. рис. 1), где и суть проекции точки М на оси Ох и Оу, обозначает величину отрезка оси абсцисс, - величину отрезка оси ординат. Число х называется абсциссой точки М, число у - ординатой этой же точки. Символ М(х; у) обозначает, что точка М имеет абсциссой число х, а ординатой число у.

Ось Оу разделяет всю плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Ох, называется правой, другая - левой. Точно так же ось Оу разделяет плоскость на две полуплоскости; та из них, которая расположена в положительном направлении оси Оу, называется верхней, другая нижней.

Обе координатные оси вместе разделяют плоскость на четыре четверти, которые нумеруют по следующему правилу: первой координатной четвертью называется та, которая лежит одновременно в правой и в верхней полуплоскости, второй - лежащая в левой и в верхней полуплоскости, третьей - лежащая в левой и в нижней полуплоскости, четвертой - лежащая в правой и в нижней полуплоскости.