![]()

![]()
![]()
Глава 3. Определители третьего порядка
Пусть дана квадратная таблица
из девяти чисел ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
 . (1)
. (1)
Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом

Глава 3. Определители третьего порядка
Пусть дана квадратная таблица из девяти чисел
,
,
,
,
,
,
,
,
:
. (1)
Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом
и определяемое равенством
 . (2)
. (2)
Числа ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() называются
элементами определителя. Элементы
называются
элементами определителя. Элементы ![]() ,
, ![]() ,
, ![]() расположены на диагонали
определителя, называемой главной; элементы
расположены на диагонали
определителя, называемой главной; элементы ![]() ,
, ![]() ,
, ![]() составляют его побочную
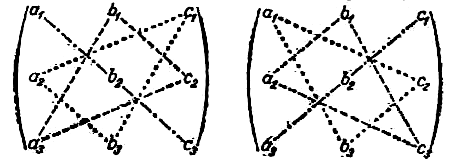
диагональ. Для практики вычислений полезно
заметить, что первые три слагаемые в правой части
равенства (2) представляют собой произведения
элементов определителя, взятых по три так, как
показано различными пунктирами на
нижеприводимой схеме слева.
составляют его побочную
диагональ. Для практики вычислений полезно
заметить, что первые три слагаемые в правой части
равенства (2) представляют собой произведения
элементов определителя, взятых по три так, как
показано различными пунктирами на
нижеприводимой схеме слева.
Чтобы получить следующие три члена правой части равенства (2), нужно перемножить элементы определителя по три так, как показано различными пунктирми на той же схеме справа, после чего у каждого из найденных произведений изменить знак.
![]()
![]()
| Текст издания: | © Д.В.Клетеник "Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998. |
|
| Решение задач: | © Кирилл Кравченко,
http://a-geometry.narod.ru/. Все права принадлежат мне, если не оговорено иное ;-) |
![]()