






Глава 1. Определители второго порядка и система
двух уравнений первой степени с двумя
неизвестными
Пусть дана квадратная таблица
из четырех чисел 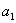 ,
, 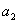 ,
, 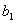 ,
, 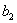 :
:
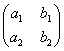 . (1)
. (1)
Число 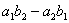 называется
определителем второго порядка, соответствующего
таблице (1). Этот определитель обозначается
символом
называется
определителем второго порядка, соответствующего
таблице (1). Этот определитель обозначается
символом 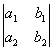 ; соотвественно имеем
; соотвественно имеем
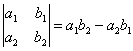 . (2).
. (2).
Числа 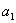 ,
, 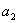 ,
, 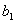 ,
, 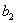 называются
элементами определителя. Говорят, что элементы
называются
элементами определителя. Говорят, что элементы 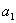 ,
, 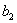 лежат на главной
диагонали определителя,
лежат на главной
диагонали определителя, 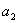 ,
, 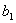 - на побочной. Таким образом,
определитель второго порядка равен разности
между произведениями элементов, лежащих на
главной и побочной диагоналях. Например,
- на побочной. Таким образом,
определитель второго порядка равен разности
между произведениями элементов, лежащих на
главной и побочной диагоналях. Например,
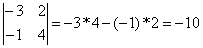 .
.
Рассмотрим систему двух уравнений
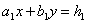 ,
, 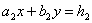 (3)
(3)
с двумя неизвестными x,
y. (Коэффициенты 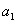 ,
, 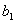 ,
, 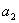 ,
, 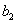 и свободные
члены
и свободные
члены 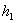 ,
, 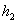 предположим данными.) Введем обозначения
предположим данными.) Введем обозначения
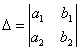 ,
, 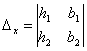 ,
, 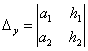 . (4)
. (4)
Определитель 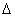 , составленный из
коэффициентов при неизвестных системы (3),
называется определителем этой системы.
Определитель
, составленный из
коэффициентов при неизвестных системы (3),
называется определителем этой системы.
Определитель 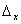 получается путем замены
элементов первого столбца определителя
получается путем замены
элементов первого столбца определителя 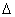 свобдными членами системы (3); определитель
свобдными членами системы (3); определитель 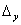 при помощи замены свободными членами системы (3)
элементов его второго столбца.
при помощи замены свободными членами системы (3)
элементов его второго столбца.
Если 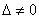 , то система (3) имеет
единственное решение; оно определяется
формулами
, то система (3) имеет
единственное решение; оно определяется
формулами
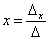 ,
,  .
.
Если 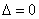 и при этом хотя бы один из
определителей
и при этом хотя бы один из
определителей 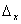 ,
, 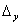 отличен от нуля, то система (3) совсем не имеет
решений (как говорят, уравнения этой системы
несовместны).
отличен от нуля, то система (3) совсем не имеет
решений (как говорят, уравнения этой системы
несовместны).
Если же 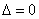 , но также
, но также 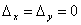 ,
то система (3) имеет бесконечно много решений (в
этом случае одно из уравнений системы есть
следствие другого).
,
то система (3) имеет бесконечно много решений (в
этом случае одно из уравнений системы есть
следствие другого).
Пусть в уравнениях системы (3) 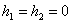 ;
тогда система (3) будем иметь вид:
;
тогда система (3) будем иметь вид:
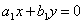 ,
, 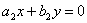 . (6)
. (6)
Система уравнений вида (6) называется
однородной; она всегда имеет нулевое решение; x=0, y=0. Если 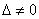 , то это решение
является единственным; если же
, то это решение
является единственным; если же 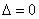 , т о система (6),
кроме нулевого, имеет бесконечно много других
решений.
, т о система (6),
кроме нулевого, имеет бесконечно много других
решений.





| Текст издания: |
© Д.В.Клетеник "Сборник задач по
аналитической геометрии". М., Наука, Физматлит,
1998. |
 |
| Решение задач: |
© Кирилл Кравченко,
http://a-geometry.narod.ru/.
Все права принадлежат мне, если не оговорено иное ;-) |

Сайт управляется системой
uCoz![]()

![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() :
: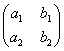 . (1)
. (1)![]() называется
определителем второго порядка, соответствующего
таблице (1). Этот определитель обозначается
символом
называется
определителем второго порядка, соответствующего
таблице (1). Этот определитель обозначается
символом 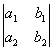 ; соотвественно имеем
; соотвественно имеем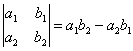 . (2).
. (2).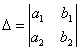 ,
, 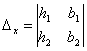 ,
, 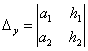 . (4)
. (4)