Глава 30. Линейные операции над векторами

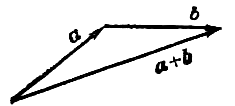
Суммой двух векторов и называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правильно треугольника). Построение суммы изображено на рис. 1.

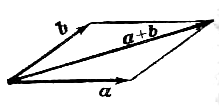
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы и приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала и (рис. 2). Отсюда сразу следует, что .

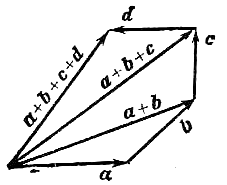
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов , , , ).

Разность двух векторов и называется вектор, который в сумме с вектором составляет вектор . Если два вектора и приведены к общему началу, то разность их есть вектор, идущий из конца («вычитаемого») к концу («уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом , то другой обозначается символом . Легко видеть, что . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».

Произведение (или также ) вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа ; он параллелен вектору или лежит с ним на одной прямой и направлен так же, как вектор , если - число положительное, и противоположно вектору , если - число отрицательное.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Имеют место следующие две основные теоремы о проекциях векторов:

1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:

2). При умножении вектора на число его проекция умножается на то же число:

.

В частности, если

, ,

то

,

и

.

Если , то для любого числа

.

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов

, ,

является пропорциональность их координат:

.

Тройка векторов , , называется координатным базисом, если эти векторы удовлетворяют следующим условиям:

1). Вектор лежит на оси Ох, вектор - на оси Оу, вектор - на оси Oz;

2). Каждый из векторов , , направлен по своей оси в положительную сторону;

3). Векторы , , единичные, то есть , , .

Каким бы ни был вектор , он всегда может быть разложен по базису , , , то есть может быть представлен в виде

;

коэффициенты этого разложения являются координатами вектора (то есть X, Y, Z суть проекции вектора на координатные оси).

Текст издания:	© Д.В.Клетеник "Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998.
Решение задач:	© Кирилл Кравченко, http://a-geometry.narod.ru/. Все права принадлежат мне, если не оговорено иное ;-)