Глава 29. Понятие вектора. Проекции вектора

Направленные отрезки принято называто также геометрическими векторами или просто векторами. Вектор как направленный отрезок мы будем по-прежнему записывать в тексте двумя большими латинскими буквами с общей чертовй наверху при условии, что первая из них обозначает начало, вторая - конец вектора. Наряду с этим мы будем также обозначать вектор одной малой латинской буквой полужирного шрифта, которая на чертежах ставится у конца стрелки, изображающей вектор (рис. 1, где изображен вектор а с началом А и концом В). Начало вектора часто будет называться таже его точкой приложения.

Векторы называются равными, если они имеют одинаковые длины, лежат на параллельных прямых или на одной прямой и направлены в одну сторону.

Число, равное длине вктора (при заданном масштабе), называется его модулем. Модуль вектора a обозначается символом или а. Если , то вектор называется единичным.

Единичный вектор, имеющий одинаковое направление с данным вектором , называется ортом вектора и обозначается обычно символом .

Проекцией вектора на ось u называется число, равное величине отрезка оси u, где точка является проекцией точки А на ось u, а - проекцией точки В на эту ось.

Проекция вектора на ось u обозначается символом . Если вектор обозначен символом , то его проекцию на ось u принято обозначать: .

Проекция вектора на ось u выражается через его модуль и угол наклона к оси u формулой

.

Проекции произвольного вектора на оси некоторой заданной системы координат в дальнейшем обозначаются буквами X, Y, Z. Равенство ={X, Y, Z} означает, что числа X, Y, Z являются проекциями вектора на координатные оси. Вектор, для которого X=Y=Z=0, называется нулевым и обозначается .

Проекции вектора на координатные оси называются также его (декартовыми) координатами. Если даны две точки (, , ) и (, , ), являющиеся соответственно началом и концом вектора , то его координаты X, Y, Z определяются по формулам , , .

Формула

(2)

позволяет по координатам вектора определить его модуль.

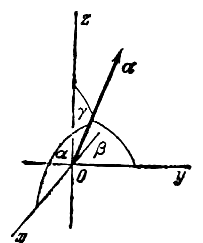
Если , , - углы, которые составляет вектор с координатными осями (см. рис. 2), то , , называются направляющими косинусами вектора .

Вследствие формулы (1)

, , .

Отсюда, и из формулы (2) следует, что

.

Последнее равенство позволяет определить один из углов , , , если известны два других.

748		Вычислить модуль вектора ={6; 3; -2}.
749		Даны две координаты вектора X=4, Y=-12. Определить его третью координату Z при условии, что =13.
750		Даны точки A(3; -1; 2), B(-1; 2; 1). Найти координаты векторов и .
751		Определить точку N, с которой совпадает конец вектора ={3; -1; 4}, если его начало совпадает с точкой М(1; 2; -3).
752		Определить начало вектора ={2; -3; -1}, если его конец совпадает с точкой (1; -1; 2).
753		Дан модуль вектора =2 и углы =450, =600, =1200. Вычислить проекции вектора на координатные оси.
754		Вычислить направляющие косинусы вектора ={12; -15; -16}.
755		Вычислить направляющие косинусы вектора ={3/13; 4/13; 12/13}.
756		Может ли вектор составлять с координатными осями следующие углы:
	756.1	=450, =600, =1200;
	756.2	=450, =1350, =600;
	756.3	=900, =1500, =600.
757		Может ли вектор составлять с двумя координатными осями следующие углы:
	757.1	=300, =450;
	757.2	=600, =600:
	757.3	=1500, =300.
758		Вектор составляет с осями Ox и Oz углы =1200 и =450. Какой угол он составляет с осью Oy?
759		Вектор составляет с координатными осями Ox и Oy углы =600, =1200. Вычислить его координаты при условии, что =2.
760		Определить координаты точки М, если ее радиус-вектор составляет с координатными осями одинаковые углы и его модуль равен 3.