Глава 18. Эллипс

Глава 18. Эллипс

Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами и , расстояние между ними - через 2с. По определению эллипса или .

Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид

(1)

где ; очевидно, . Уравнение вида (1) называется каноническим уравнением эллипса.

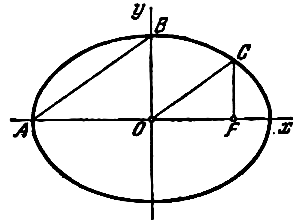
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью.

Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.

Число

где а - большая полуось, называется эксцентриситетом эллипса. Очевидно, (для окружности ). Если М(x; y) - произвольная точка эллипса, то отрезки и (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам

, .

Если эллипс определен уравнением (1) и , то прямые

,

(рис.) называются директрисами эллипса (если , то директрисы определяются уравнениями , .

Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:

Если две плоскости и образуют острый угол , то проекциейй на плоскость окружности радиуса a, лежащей на плоскости , является эллипс с большой полуосью а; малая полуось b этого эллипса определяется по формуле

(рис.).

Если круглый цилиндр имеет в качестве направляющей окружность радиуса b, то в сечении этого цилиндра плоскостью, наклоненной к оси цилиндра под острым углом , будет эллипс, малая полуось которого рвна b; большая полуось а этого эллипса определяется по формуле

(рис.).

444 Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:
444.1 его полуоси ранвы 5 и 2;
444.2 его большая ось равна 10, а расстояние между фокусами 2c=8;
444.3 его малая ось равна 24, а расстояние между фокусами 2c=10;
444.4 расстояние между его фокусами 2c=6 и эксцентриситет e=3/5.
444.5 его большая ось равна 20, а эксцентриситет e=3/5.
444.6 его малая ось равна 10, а эксцентриситет e=12/13;
444.7 расстояние между его директрисами равно 5 и расстояние между фокусами 2c=4;
444.8 его большая ось равна 8, а расстояние между директрисами равно 16;
444.9 его малая ось равна 6, а расстояние между директрисами равно 13;
444.10 расстояние между его директрисами равно 32 и e=1/2.
445 Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично начала координат, зная, кроме того, что:
445.1 его полуоси равны соответственно 7 и 2;
445.2 его большая ось равна 10, а расстояние между фокусами 2c=8;
445.3 расстояние между его фокусами 2c=24 и эксцентриситет e=12/13.
445.4 его малая ось равна 16, а эксцентриситет e=3/5.
445.5 расстояние между его фокусами 2c=6 и расстояние между директрисами равно 50/3;
445.6 расстояние между его директрисами равно 32/3 и эксцентриситет e=3/4.
446 Определить полуоси каждого из следующих эллипсов:
446.1  ;
446.2 ;
446.3 ;
446.4 ;
446.5  ;
446.6 ;
446.7 ;
446.8 ;
446.9 ;
446.10 .
447 Дан эллипс . Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.
448 Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , а две другие совпадают с концами его малой оси.
449 Дан эллипс . Найти его полуоси, фокусы, эксцентриситет, уравнения директрис.
450 Вычислить площадь четырехугольника, две вершины которого лежат в фокусах эллипса , две другие лежат с концами его малой оси.
451 Вычислить расстояние от фокуса F(c; 0) эллипса до односторонней с этим фокусом директрисы.
452 Пользуясь одним циркулем, построить фокусы эллипса (считая, что изображены оси координат и задана масштабная единица).
453 На эллипсе найти точку, абсцисса которых равна –3.
454 Определить, какие из точек A1(-2; 3), A2(2; -2), A3(2; -4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3; -2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе , какие внутри и какие вне его.
455 Установить, какие линии опеределяются следующими уравнениями. Изобразить эти линии на чертеже.
455.1 ;
455.2 ;
455.3 ;
455.4 .
456 Эксцентриситет эллипса e=2/3, фокальный радиус точки М эллипса равен 10. Вычислить расстояние от точки М до односторонней с этим фокусом директрисы.
457 Эксцентриситет эллипса e=2/5, расстояние от точки эллипса до директрисы равно 20. Вычислить расстояние от точки М до фокуса, односторонней с этой директрисой.
458 Дана точка М1(2; -5/3) на эллипсе ; составить уравнения прямых, на которых лежат фокальные радиусы точки М1.
459 Убедившись, что точка M1(-4; 2,4) лежит на эллипсе , определить фокальные радиусы точки М1.
460 Эксцентриситет эллипса e=1/3, центр его совпадает с началом координат, один из фокусов (-2; 0). Вычислить расстояние от точки М1 эллипса с абсциссой, равной 2, до директрисы, односторонней с данным фокусом.
461 Эксцентриситет эллипса e=1/2, центр его совпадает с началом координат, одна из директрис дана уравнением x=16. Вычислить расстояние от точки M1 эллипса с абсциссой, равной –4, до фокуса, одностороннего с данной директрисой.
462 Определить точки эллипса , расстояние которых до правого фокуса равно 14.
463 Определить точки эллипса , расстояние которых до левого фокуса равно 2,5.
464 Через фокус эллипса проведен перпендикуляр к его большой оси. Определить расстояния от точек пересечения этого перпендикуляра с эллипсом до фокусов.
465 Составить уравнения эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны:
465.1 точка М1(; 2) эллипса и его малая полуось b=3;
465.2 точка М1(2; -2) эллипса и его большая полуось a=4;
465.3 точки М1(4; ) и М2(; 3) эллипса;
465.4 точка М1(; -1) эллипса и его эксцентриситет e=2/3;
465.5 точка М1(2; -5/3) эллипса и его эксцентриситет e=2/3;
465.6 точка М1(8; 12) эллипса и расстояние r1=20 от нее до левого фокуса.
465.7 точка М1(; 2) эллипса и расстояние между его директрисами, равное 10.
466 Определить эксцентриситет e эллипса, если:
466.1 его малая ось видна из фокусов под углом 600;
466.2 отрезок между фокусами виден и вершин малой оси под прямым углом;
466.3 расстояние между директрисами в три раза больше расстояния между фокусами;
466.4 отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вершиной эллипса пополам.
467 Через фокус F эллипса проведен перпендикуляр к его большой оси (см. рис.). Определить, при каком значении эксцентриситета эллипса отрезки и будут параллельны.
468 Составить уравнение эллипса с полуосями a, b и центром C(x0, y0), если известно, что оси симметрии эллипса параллельны осям координат.
469 Эллипс касается оси абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
470 Точка С(-3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
471 Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис:
471.1 ;
471.2 ;
471.3 .
472 Установить, какие линии определяются следующими уравнениями. Изобразить эти линии на чертеже.
472.1  ;
472.2 ;
472.3 ;
472.4 .
473 Составить уравнение эллипса, зная, что:
473.1 его большая ось равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2 его малая ось равна 2 и фокусы суть F1(-1; -1), F2(1; 1);
473.3 его фокусы суть F1(-2; 3/3), F2(2; -3/2) и эксцентриситет e=.
473.4 его фокусы суть F1(1; 3), F2(3; 1) и расстояние между директрисами равно .
474   Составить уравнение эллипса, если известны его эксцентриситет , фокус F (-4; 1) и уравнение соответствующей директрисы
475 Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(-4; 1) и уравнение соответствующей директрисы .
476 Точка А(-3; -5) лежит на эллипсе, фокус которого F(-1; -4), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.
477 Составить уравнение эллипса, если известны его эксцентриситет e=1/2, фокус F(3; 0) и уравнение соответствующей директрисы .
478 Точка M1(2; -1) лежит на эллипсе, фокус которого F(1; 0), а соответствующая директриса дана уравнением . Составить уравнение этого эллипса.
479 Точка M1(3; -1) является концом малой оси эллипса, фокусы которого лежат на прямой . Составить уравнение этого эллипса, зная его эксцентриситет e=.
480 Найти точки пересечения прямой и эллипса .
481 Найти точки пересечения прямой и эллипса .
482 Найти точки пересечения прямой и эллипса .
483 Определить, как расположена прямая относительно эллипса: пересекает ли, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями:
483.1 , ;
483.2 , ;
483.3 , .
484 Определить, при каких начениях m прямая :
484.1 пересекает эллипс ;
484.2 касается его;
484.3 проходит вне этого эллипса.
485 Вывести условие, при котором прямая касается эллипса .
486 Составить уравнение касательной к эллипсу в его точке M1(x1; y1).
487 Доказать, что касательные к эллипсу , проведенные в концах одного и того же диаметра, параллельны. (Диаметром эллипса называется его хорда, проходящая через его центр).
488 Составить уравнения касательных к эллипсу, параллельных прямой .
489 Составить уравнения касательных к эллипсу , перпендикулярных к прямой .
490 Провести касательные к эллипсу параллельно прямой и вычислить расстояние d между ними.
491 На эллипсе найти точку М1, ближайшую к прямой , и вычислить расстояние d от точки М1 до этой прямой.
492 Из точки А(10/3; 5/3) проведены касательные к эллипсу . Составить их уравнения.
493 Из точки С(10; -8) проведены касательные к эллипсу . Составить уравнение хорды, соединяющей точки касания.
494 Из точки Р(-16; 9) проведены касательные к эллипсу . Вычислить расстояние d от точки Р до хорды эллипса, соединяющей точки касания.
495 Эллипс проходит через точку А(4; -1) и касается прямой . Составить уравнение этого эллипса при условии, что его оси совпадают с осями координат.
496 Составить уравнение эллипса, касающегося двух прямых , , при условии, что его ося совпадают с осями координат.
497 Доказать, чо произведение расстояний от центра эллипса до точки пересечения любой его касательной с фокальной осью и до основания перпендикуляра, опущенного из точки касания на фокульную ось, если величина постоянная, равная квадрату большой полуоси эллипса.
498 Доказать, что произвдение расстояний от фокусов до любой касательной к эллипсу равно квадрату малой полуоси.
499 Прямая касается эллипса, фокусы которого находятся в точках F1(-3; 0), F2(3; 0). Составить уравнение этого эллипса.
500 Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу и его малая полуось b=2.
501 Доказать, что прямая, касающаяся эллипса в некоторой точке М, составляет равные углы с фокальными радиусами F1M, F2M и проходит вне угла F1MF2.
502 Из левого фокуса эллипса под тупым углом к оси Ox направлен луч света. Известно, что . Дойдя до эллипса, луч на него отразился. Составить уравнение прямой, на которой лежит отраженный луч.
503 Определить точки пересечения эллипсов , .
504 Убедившись, что эллипсы , () пересекаются в четырех точках, лежающих на окружности с центром в начале координат, определить радиус R этой окружности.
505 Плоскости и образуют угол =300. Опредлить полуоси эллипса, полученного проектированием на плоскость окружности радиуса R=10,лежащей на плоскости .
506 Эллипс, малая полуось которого равна 6, является проекцией окружности радиуса R=12. Опредилть угол между плоскостями, в которых лежат эллипс и окружность.
507 Направляющей круглого цилиндра является окружность радиуса R=8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклоненной к его оси под уголом =300.
508 Направляющей круглого цилиндра является окружность радиуса R=. Определить, под каким углом к оси цилиндра нужно его пересечь плоскостью, чтобы в сечении получить эллипс с большой полуосью a=2.
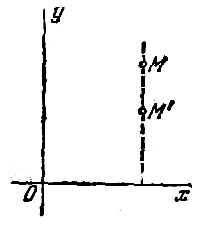
509 Равномерным сжатием (или равномерным растяжением) плоскости к оси абсцисс называется такое преобразование точек плоскости, при котором произвольная точка M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что x’=x, y’=qy, где q>0 – постоянная, называемая коэффициентом равномерного сжатия. Аналогично рпи помощи уравнения x’=qx, y’=y определяется равномерное сжатия плоскости к оси Oy (рис. 2). Определить, в какую линию преобразуется окружность , если коэффициент равномерного сжатия плоскости к оси абсцисс q=4/5.
510 Коэффициент равномерного сжатия плоскости к оси Oy равен 3/4. Определить уравнение линии, в которую при таком сжатии преобразуется эллипс .
511 Найти уравнение линии, в которую преобразуется эллипс при двух последовательных равномерных сжатиях плоскости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ox и Oy равны соответственно 4/3 и 6/7.
512 Определить коэффициент q равномерного сжатия плоскости к оси Ox, при котором эллипс преобразуется в эллипс .
513 Определить коэффициент q равномерного сжатия плоскости к оси Oy, при котором эллипс преобразуется в эллипс .
514 Определить коэффициенты q1, q2 двух последовательных равномерных сжатий плоскости к осям Ox и Oy, при которых эллипс преобразуется в окружность .

Текст издания: © Д.В.Клетенник "Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998
Решение задач: © 2004-2013, Кирилл Кравченко, http://a-geometry.narod.ru/, http://kirill-kravchenko.narod.ru/		 Яндекс.Метрика