![]()

![]()
![]()
Глава 5. Деление отрезка в данном отношении
Если точка М(x; y) лежит на прямой, проходящей через две данные точки![]() ,
,
![]() .
.
Если точка М является серединой отрезка
![]() ,
то ее координаты определяются по формулам
,
то ее координаты определяются по формулам
![]() ,
,
![]() .
.
| 86 | Даны концы А(3; -5), В(-1; 1) однородного стержня. Определить координаты его центра масс. | |
| 87 | Центр мас однородного стержня находится в точке М(1; 4), один из его концов Р(-2; 2). Определить координаты точки Q – другого конца этого стержня. | |
| 88 | Даны вершины треугольника А(1; -3), В(3; -5), С(-5; 7). Определить середины его сторон. | |
| 89 | Даны точки А(3; -1), С(2; 1). Определить: | |
| 89.1 | Координаты точки М, симметричной точке А относительно точки В; | |
| 89.2 | Координаты точки N, симметричной точке В относительно точки А. | |
| 90 | Точки А(2; -1), N (-1; 4), P(-2; 2) являются серединами сторон треугольника. Определить его вершины. | |
| 91 | Даны три вершины параллелограмма А(3; -5), B(5; -3), C(-1; 3). Определить четвертую вершину D, противоположную B. | |
| 92 | Даны две смежные вершины параллелограмма А(-3; 5), B(1; 7) и точка пересечения его диагоналей M(1; 1). Определить две другие вершины. | |
| 93 | Даны три вершины А(2; 3), B(4; -1), C(0; 5) параллелограмма ABCD. Найти его четвертую вершину D. | |
| 94 | Даны вершины треугольника A(1; 4), B(3; -9), C(-5; 2). Определить длину его медианы, проведенной из вершины B. | |
| 95 | Отрезок, ограниченный точками A(1; -3), B(4; 3) разделен на три равные части. Определить координаты точек деления. | |
| 96 | Даны вершины треугольника A(2; -5), B(1; -2), C(4; 7). Найти точку пересечения биссектрисы его внутреннего угла при вершине В со стороной АС. | |
| 97 | Даны вершины треугольника A(3; -5), B(-3; 3), C(-1; -2). Определить длину биссектрисы его внутреннего угла при вершине А. | |
| 98 | Даны вершины треугольника А(-1; -1), B(3; 5), C(-4; 1). Найти точку пересечения биссектрисы его внешнего угла при вершине А с продолжением стороны ВС. | |
| 99 | Даны вершины треугольника А(3; -5), B(1; -3), C(2; -2). Определить длину биссектрисы его внешнего угла при вершине В. | |
| 100 | Даны точки А(1; 1), В(3; 3), С(4; 7). Определить
отношение |
|
| 101 | Определить координаты концов А и В отрезка, который точками P(2; 2), Q(1; 5) разделен на три равные части. | |
| 102 | Прямая проходит через точки M1(-12; -13), M2(-2; -5). На этой прямой найти точку, абсцисса которой равна 3. | |
| 103 | Прямая проходит через точки M(2; -3), N(-6, 5). На этой прямой найти точку, ордината которой равна –5. | |
| 104 | Прямая проходит через точки A(7; -3), B(23; -6). Найти точку пересечения этой прямой с осью абсцисс. | |
| 105 | Прямая проходит через точки A(5; 2), B(-4; -7). Найти точку пересечения этой прямой с осью ординат. | |
| 106 | Даны вершины четырехугольника А(-3; 12), B(3; -4), C(5; -4), D(5; 8). Определить, в каком отношении его диагональ AC делит диагональ BD. | |
| 107 | Даны вершины четырехугольника A(-2; 14), B(4; -2), C(6; -2), D(6; 10). Определить точку пересечения его диагоналей AC и BD. | |
| 108 | Даны вершины однородной треугольной пластинки A(x1; y1), B(x2; y2), C(x3; y3). Определить координаты ее центра масс. Центр масс находится в точке пересечения медиан. | |
| 109 | Точка M пересечения медиан треугольника лежт на оси абсцисс, две вершины его – точки А(2; -3) и B(-5; 1), третья вершина C лежит на оси ординат. Определить координаты точек M и C. | |
| 110 | Даны вершины однородной треугольной пластинки A(x1; y1), B(x2; y2), C(x3; y3). Если соединить середины ее сторон, то образуется новая однородная треугольная пластинка. Доказать, что центры масс обеих пластинок совпадают. | |
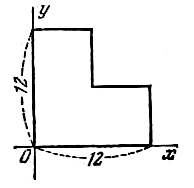
| 111 | Однородная пластинка имеет форму
квадрата со стороной, равной 12, в которой сделан
квадратный вырез, прямые разрезы проходят через
центр квадрата, оси координат направлены по
ребрам пластинки (рис.). Определить центр масс
этой пластинки.
|
|
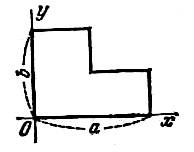
| 112 | Однородная пластинка имеет форму
прямоугольника со сторонами, равными a и b,
в котором сделан прямоугольный вырез; прямые
разреза проходят через центр, оси координат
направлены по ребрам пластинки (Рис). Определить
центр масс этой пластинки.
|
|
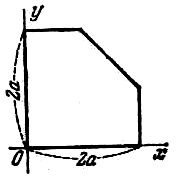
| 113 | Однородная пластинка имеет форму
квадрата со стороной, равной 2a, от которого
отрезан треугольник; прямая разреза соединяет
середины двух смежных сторон, оси координат
направлены по ребрам пластинки (Рис). Определить
центр масс пластинки.
|
|
| 114 | В точках A(x1; y1), B(x2; y2), C(x3; y3) сосредоточены массы m, n, p. Определить координаты центра тяжести этой системы. | |
| 115 | Точки A(4; 2), B(7; -2), C(1; 6) являются вершинами треугольника, сделанного из однородной проволоки. Определить центр масс этого треугольника. |
![]()
|
Текст издания: © Д.В.Клетенник "Сборник
задач по аналитической геометрии". М., Наука, Физматлит, 1998 Решение задач: © 2004-2013, Кирилл Кравченко, http://a-geometry.narod.ru/, http://kirill-kravchenko.narod.ru/ |
|
![]()