






Глава 31. Скалярное произведение векторов
Скалярным
произведением двух векторов называется число,
равное произведению модулей этих векторов на
косинус угла между ними.
Скалярное произведение векторов 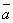 ,
, 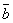 обозначается
символом
обозначается
символом 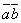 (порядок записи сомножителей
безразличен, то есть
(порядок записи сомножителей
безразличен, то есть 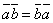 ).
).
Если угол между векторами 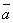 ,
, 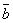 обозначить через
обозначить через
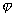 ,
то их скалярное произведение можно выразить
формулой
,
то их скалярное произведение можно выразить
формулой
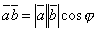 (1)
(1)
Скалярное произведение векторов 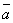 ,
, 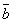 можно выразить
также формулой
можно выразить
также формулой
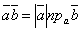
, или 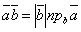 .
.
Из формулы (1) следует, что 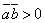 , если
, если 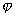 -
острый угол,
-
острый угол, 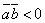 , если
, если 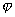 - тупой угол;
- тупой угол; 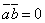 в том и только в
том случае, когда векторы
в том и только в
том случае, когда векторы 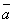 и
и 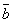 перпендикулярны
(в частности,
перпендикулярны
(в частности, 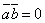 , если
, если 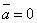 или
или 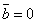 ).
).
Скалярное произведение 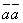 называется скалярным квадратом вектора и
обозначается символом
называется скалярным квадратом вектора и
обозначается символом 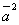 . Из формулы (1)
следует, что скалярный квадрат вектора равен
квадрату его модуля:
. Из формулы (1)
следует, что скалярный квадрат вектора равен
квадрату его модуля:
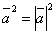 .
.
Если векторы 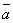 и
и 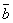 заданы своими
координатами:
заданы своими
координатами:
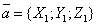 ,
, 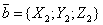 ,
,
то их скалярное произведение может
быть вычислено по формуле
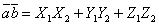 .
.
Отсюда следует необходимое и
достаточное условие перпендикулярности двух
векторов
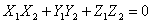 .
.
Угол 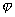 между векторами
между векторами
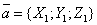 ,
, 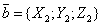 ,
,
дается формулой 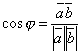 , или в
координатах
, или в
координатах
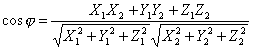 .
.
Проекция произвольного вектора 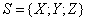 на какую-нибудь ось u
определяется формулой
на какую-нибудь ось u
определяется формулой
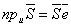 ,
,
где 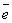 - единичный вектор, направленный
по оси u. Если даны углы
- единичный вектор, направленный
по оси u. Если даны углы 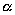 ,
, 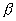 ,
, 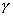 , которые оси u
составляет с координатными осями, то
, которые оси u
составляет с координатными осями, то 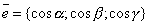 и
для вычисления вектора
и
для вычисления вектора 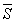 может служить
формула
может служить
формула
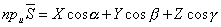 .
.





| Текст издания: |
© Д.В.Клетеник "Сборник задач по
аналитической геометрии". М., Наука, Физматлит,
1998. |
 |
| Решение задач: |
© Кирилл Кравченко,
http://a-geometry.narod.ru/.
Все права принадлежат мне, если не оговорено иное ;-) |

Сайт управляется системой
uCoz![]()

![]()
![]()
![]() ,
, ![]() обозначается
символом
обозначается
символом ![]() (порядок записи сомножителей
безразличен, то есть
(порядок записи сомножителей
безразличен, то есть ![]() ).
).![]() ,
, ![]() обозначить через
обозначить через
![]() ,
то их скалярное произведение можно выразить
формулой
,
то их скалярное произведение можно выразить
формулой![]() (1)
(1)![]() ,
, ![]() можно выразить
также формулой
можно выразить
также формулой![]()
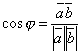 , или в
координатах
, или в
координатах